How to Estimate Max TPS from TPM

It’s good to understand the TPS (transaction per second) of a service. But sometimes we only have TPM (transaction per minute) metrics. It may be because we don’t have TPS metrics at all since they need resources to compute, or they have been deleted because storing all the historical per second metrics needs a lot of storage space. So we need to estimate TPS from TPM (or even longer time period, which the method below also applies). It’s not hard to get an average TPS from TPM: just divide TPM by 60. However, because the database and the dependency services have a limit on how many concurrent requests it can handle, we also need to understand what’s the max TPS. In this article, we will explore how to do that.

We have an assumption before we go to the solution: we assume that in the time period of one minute, the requests to the service have the same probability to happen at any time. In other words, the requests are independent of the time since the last request. This describes a Poisson process, where events occur independently at a constant average rate. This is a reasonable assumption: though most services have peak requests during a day, they tend to be distributed evenly in a short period like one minute with a consistent arrival pattern.

With this assumption in mind, we can use Poisson distribution to solve this problem. The probability of how many times the event occurs in the interval of time can be solved by this:

\(P(TPS=k) = \frac{\lambda^k e^{-\lambda}}{k!}\)

\(k\) means how many times the event happens in the interval of time. \(\lambda\) means the average of times that the event will occur in the interval.

In our case, the interval of time is 1 second. So \(\lambda\) is the average TPS: \(TPM / 60\). And \(P(k)\) means the probability of the TPS during this minute.

So we have the probability of the TPS. But what we want is to find a rate limit threshold n where we can be confident that TPS won’t exceed it. If we want to know the probability that TPS is at most n in any given second, we can add all the probabilities of TPS from 0 to n:

\(P(TPS \leq n) = \sum_{k=0}^{n} P(TPS=k) = \sum_{k=0}^{n} \frac{\lambda^k e^{-\lambda}}{k!}\)

Then we can draw a graph of this function and select n that makes the probability close to our desired confidence level (e.g., 0.95 for 95% confidence). I recommend Wolfram Alpha to draw the graph. Though it needs a paid version to show a clearer graph, the free version is enough for our use case.

Let’s give an example. Suppose we find our max TPM during peak time is 12000, then the average TPS during that minute is 200, which means \(\lambda = 200\). Then we can draw a graph of \(P(TPS \leq n)\) with \(\lambda = 200\):

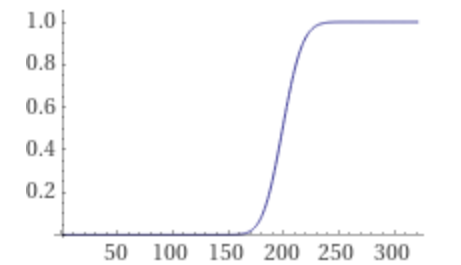
From the graph, we can see a rate limit threshold of 260 TPS gives us high confidence (close to 99%) that any given second won’t exceed this limit. And in this minute, there is about a 50% chance that the TPS will be above the average TPS of 200.

Sometimes the dependency has a throttling mechanism. It may have a target throttling configuration as TPS, but actually count the throttling number by sub-second metrics like transactions per 100ms. (Ideally this shouldn’t be the case but sometimes that happens and we don’t always have control over dependency services). In this case, we need to find the threshold for transactions per 100ms, where \(\lambda = 20\):

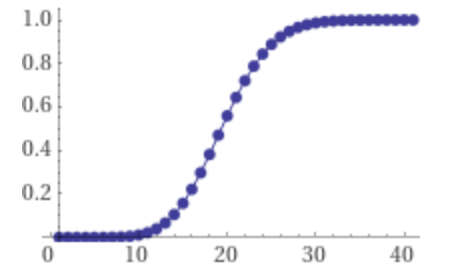
From the graph, we can see a safe threshold for transactions per 100ms would be around 36. And when we provide a target throttling TPS, we should multiply this by 10 which is 360, a lot higher than 260.

The calculation above also applies when it counts throttling numbers independently on multiple hosts. (Again, it should have a better throttling counting mechanism). For example, if the dependency service has 10 hosts and it chooses a random host to handle the request, then we should set the threshold per host, where \(\lambda\) is also 20 and target TPS configuration should be 360 instead of 260.

Update at Sep 22, 2022: Fix the formula from \(e^{-k}\) to \(e^{-\lambda}\). The graphs and results were computed with \(e^{-\lambda}\) so they are still correct.